Research projects

Recent projects

Recently (2020-2023), I worked as a Research Software Engineer in the Climate Modeling Alliance (CliMA). CliMA is a coalition of scientists, engineers, and applied mathematicians from Caltech, MIT, and NASA’s Jet Propulsion Laboratory. The CliMA team is building a new Earth system model (ESM) that leverages recent advances in the computational and data sciences to learn directly from a wealth of Earth observations from space and the ground to produce accurate climate predictions with quantified uncertainties.

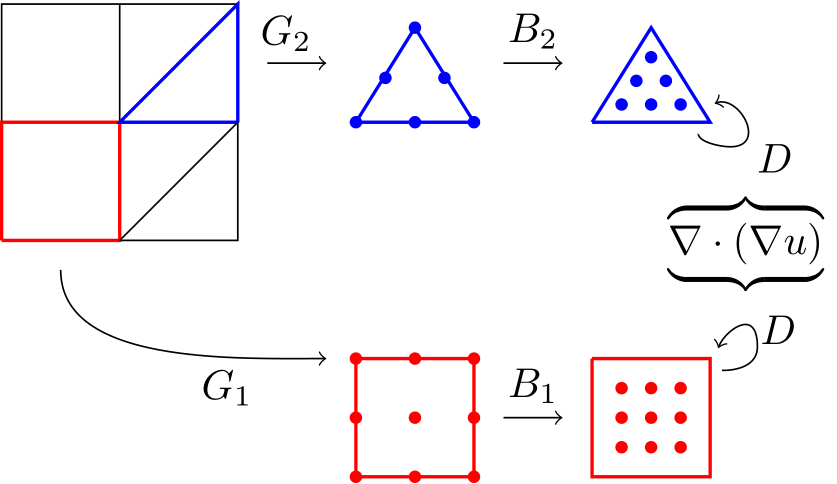
CliMA’s ESM is entirely written in the Julia language. The CliMA model targets both CPU and GPU architectures, using a common codebase. I mainly contributed to ClimaCore.jl, the open-source community library/package that constitutes the dynamical core (dycore) of the atmosphere and land models, providing discretization tools to solve the governing equations of the ESM component models. ClimaCore.jl’s high-level application programming interface (API) facilitates modularity and composition of differential operators and the definition of flexible discretizations. This, in turn, is coupled with low-level APIs that support different data layouts, specialized implementations, and flexible models for threading, to better face high-performance optimization, data storage, and scalability challenges on modern HPC architectures. I have been contributing in many aspects of the high- and low-level APIs, adding support for differential operators, several integration tests and examples, given major contributions to the documentation, and, more recently, I have been focusing on stabilization methods, such as optimization-based flux limiters.

I also controbuted extensively to other packages in the CliMA ecosystem, namely ClimaAtmos.jl, the main package for the atmosphere dynamics, and ClimaCoupler.jl, the package responsible for coupling different model components together, exchanging quantities such as fluxes, synchronizing the different systems at play.

Numerical solution of the shallow-water equations with a non-uniform mountain substrate

Numerical solution of the shallow-water equations on a cubed-sphere surface with a non-uniform mountain substrate.

Numerical solution of the advection of a slotted-cylinder tracer

Numerical solution of the trasport of a slotted-cylinder tracer on the cubed-sphere surface (plotted in lat-long grid). Purely advection-dominated problems (with no natural or numerical diffusion) discretized with high-order finite element methods suffer from oscillations due to the Gibbs phenomenon.

Numerical solution of the tranport of a slotted-cylinder tracer on the cubed-sphere surface (plotted in lat-long grid). Differently from the previous example, we can see that the addition of optimization-based flux limiters helps reducing the undesired numerical oscillations.

Postdoc project

For my postdoc, I joined the efforts of the Center for Efficient Exascale Discretizations (CEED), a co-design center of the Exascale Computing Project (ECP): a project mainly funded by the U. S. Department of Energy (DOE). I was advised by Jed Brown, PI of the PhyPID research group at CU Boulder. I collaborated in the development of libCEED, an open-source community software, which provides efficient and performance portable interfaces for representing linear and nonlinear, as well as constructing preconditioning ingredients. LibCEED offers a purely algebraic interface for matrix-free operator representation and supports run-time selection of implementations tuned for a variety of computational device types, including CPUs and GPUs. While libCEED’s focus is on high-order finite elements, the approach is algebraic and thus applicable to other discretizations in factored form. My main contributions have been on the high-level APIs, benchmark problems on spherical geometries, application examples, especially the Navier-Stokes fluids miniapp, the C-python interface, and I have been the main author of the user manual.

A schematic representation of mixed finite elements

A schematic of element restriction and basis applicator operators for elements with different topology. This sketch shows the independence of QFunctions (in this case representing a Laplacian) element resolution, topology, or basis degree..

Numerical solution of the density current problem. This is a typical test case for large-scale high-resolution atmospheric flow problems. The test case represents a falling cold air bubble that drops by convection in a neutrally stratified atmosphere.

PhD project

My PhD dissertation was mainly in the field of computational fluid dynamics, specifically to study the behavior of thin layers of complex fluids such as non-Newtonian fluids, but out of personal interest, it also contained secondary projects in which I ventured into solid mechanics and physics-based computer animation applications.

In the primary project, co-advised by Shahriar Afkhami and Lou Kondic in the Complex Flows and Soft Matter Group, I carried out an original computational investigation for thin viscoelastic films on a flat solid substrate subject to the van der Waals interaction force and the gravitational body force, in specific settings. In this work, the governing equations are obtained within a thin film approximation of the Navier-Stokes equations with Jeffreys constitutive model for viscoelastic stresses. The numerical method chosen is an implicit/explicit finite difference scheme, with adaptive time step discretization and staggered spatial grid with fixed size (software publicly available in this repository). The investigation focused on the effects of viscoelasticity, contact angle, and the substrate slippage on the dynamics of thin viscoelastic films. This study was the first of its kind that presented numerical solutions of the full nonlinear interfacial instabilities arising from a model with this level of complexity (i.e., including viscoelasticity, interaction forces, and different slip regimes) in different settings: wetting/dewetting of thin films and spreading/receding of drops.

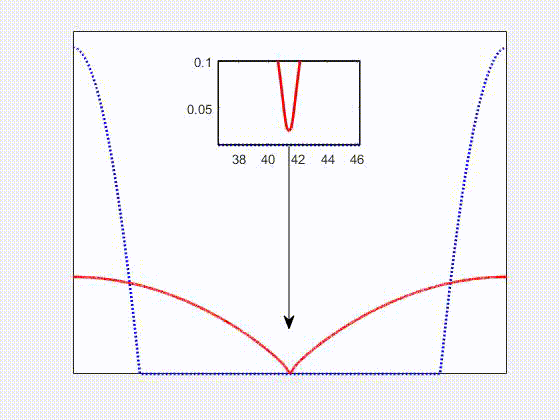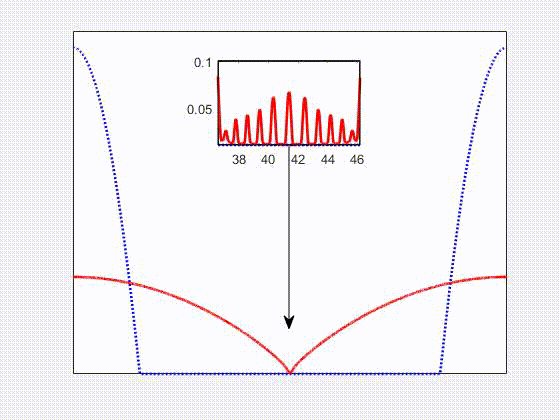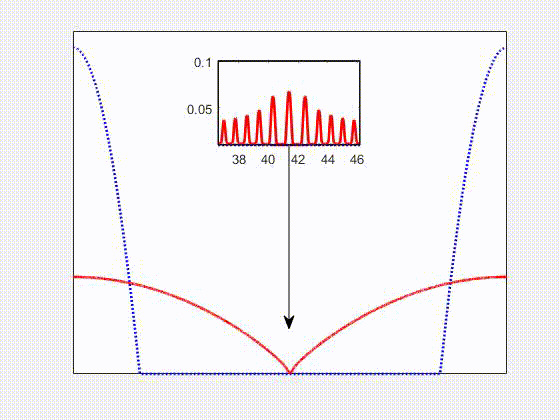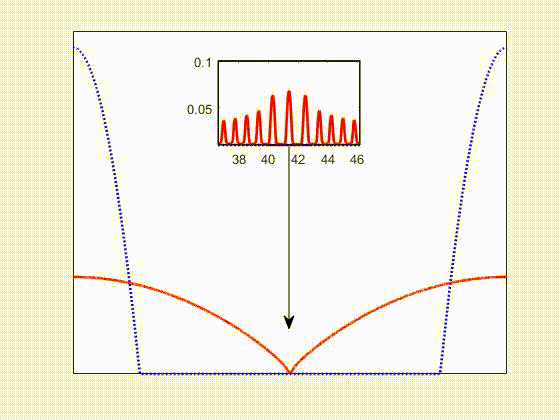
A viscoelastic dewetting film compared to a Newtonian one

Numerical solution of the dynamics of the interface instability of a viscoelastic film of Jeffreys type (red solid line), compared to a viscous film (blue dotted line), on a flat plane, sucbjected to the van der Waals interaction force.

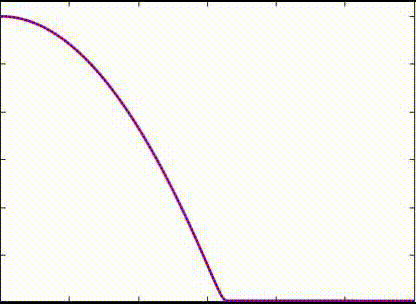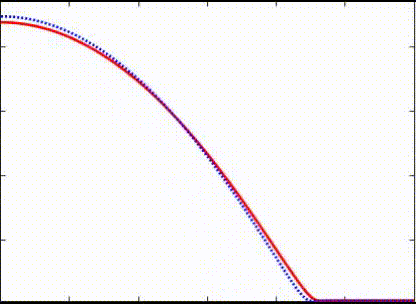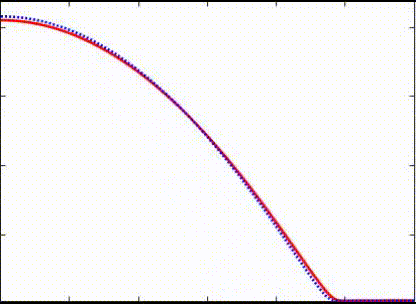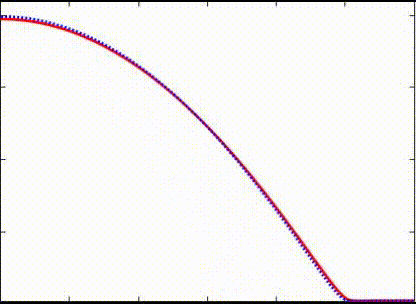
A viscoeasltic spreading drop compared to a Newtonian one

Numerical solution of the dynamics of the interface instability of a spreading viscoelastic drop of Jeffreys type (red solid line), compared to a viscous drop (blue dotted line), on a flat plane, sucbjected to the van der Waals interaction force.

A randomly perturbed inverted viscoelastic film

Numerical solution of the dynamics of the interface instability of a Jeffreys viscoelastic film perturbed by different wavelengths of random amplitude on an inverted plane, sucbjected to both the van der Waals interaction force and the gravitational body force.

In the secondary project, co-advised by Shahriar Afkhami and Shawn Chester, I independently carried out numerical simulations of the dynamics of free-boundary flows of nearly-incompressible viscoelastic membranes. This formulation is suitable to model both soft matter (e.g., gel) and thin liquid membranes. The finite element method was chosen to discretize the dynamic problem, in which the slender geometry representing the membranes is discretized by linear triangular elements under plane stress conditions.

A nearly-incompressible sheared Cook viscoelastic membrane

Numerical solution of the dynamics of a sheared Cook's membrane of Maxwell type.

A nearly-incompressible stretched viscoelastic membrane

Numerical solution of the dynamics of a stretched Maxwell membrane in drawing engineering processes.

Pixar

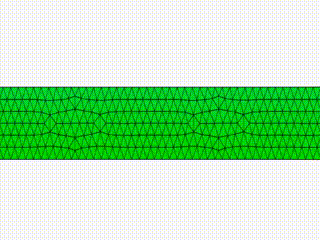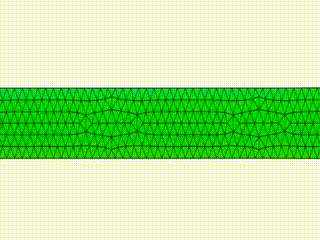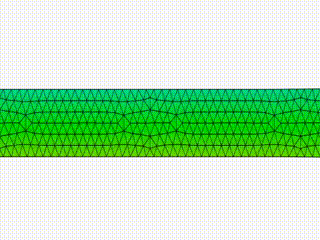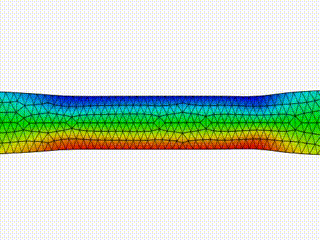
During the fourth year of my PhD program, motivated by some interest in Computer Graphics that originated during my Master’s thesis studies, I interned in the Research group at Pixar Animation Studios. As A Research Intern, I developed a proprietary C++ library for a 2D Navier-Stokes solver for viscous fluid simulations on surfaces with arbitrary curvature. I extended existing code to include different types of discretized domains (from triangular to polygonal meshes), adding support for user-defined solid obstacle (to simulate fluid-structure interactions), and boundary conditions for open meshes. The software produced for this project was prototyped as a plug-in for a third-party procedural 3D animation and special effects software for film and entertainment, Houdini by SideFX. As a second project, I also developed a proprietary C++ library to simulate the dynamics and interface instabilities of 3D thin viscous films on triangular surfaces with arbitrary curvature.

Me on the first day of my internship at Pixar.

Surface flow on a poligonal mesh with curvature

Physics-based animation of a surface viscous flow on a poligonal mesh with arbitrary curvature.

Physics-based animation of a thin viscous film flowing down a sphere.

Master project

For my master’s thesis project, I analyzed and implemented the original algorithm by Catmull-Clark for closed subdivision surfaces. The phrase subdivision surfaces, in the field of 3D Computer Graphics, refers to a class of surfaces that are obtained with the aid of computers through repeated refinements of their control points polyhedra. The Catmull-Clark subdivision algorithm works on polyhedra with arbitrary topology, and the limit-surface generated by this geometric flow is a uniform bicubic B-spline surface of class C², except at points that have a number of adjacent edges different from four, called extraordinary points, where they have C¹ continuity.

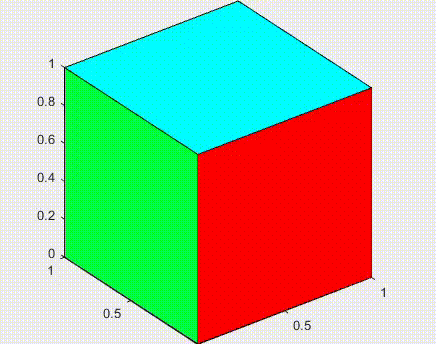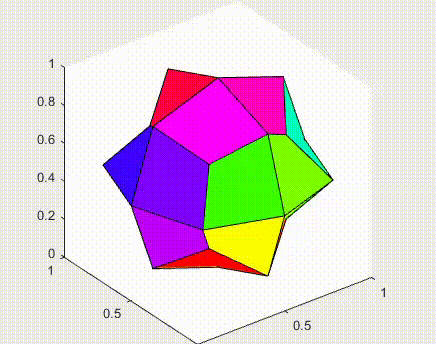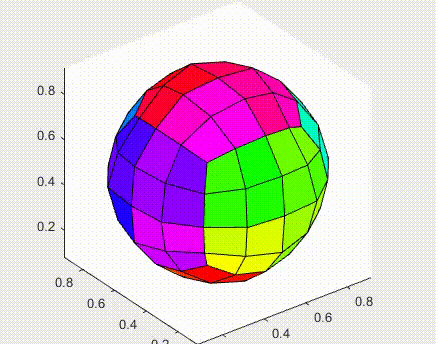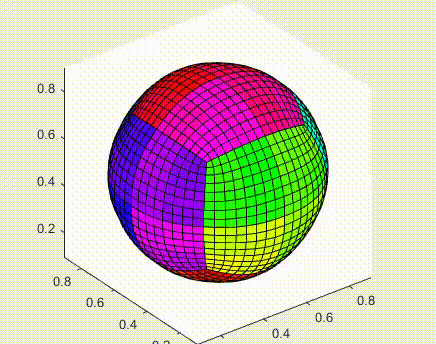
Catmull-Clark subdivision surface of a cubed-sphere

Catmull-Clark subdivision of a cubed-sphere.

Indipendent contribution: to extend the original algorithm, which only treated closed surfaces, I added support for open surfaces. In this case, the boundary conditions were implemented using the same approach as the one by Nasri (i.e. the auxiliary ghost nodes are defined by linear extrapolations of the internal nodes, similar to a reflective boundary condition in the analysis of partial differential equations).

Catmull-Clark subdivision surface of an open surface

Catmull-Clark subdivision of an open surface.